Nowak et al. take it on the chin.

Not pretty...photo from hunterseakerhk

At the end of September last year, I was attending the opening of the ISBE conference (International Society for Behavioral Ecology) in Perth, Australia when Stuart West got up to give a keynote address.  One of the first things he said was something along the lines of “I’ve been getting a lot of questions about this, but I’m not going to address the eusociality paper”, which was met by a chorus of hoots and cries from the audience.  It was a great first-hand experience of the kind of reaction that the paper by Martin Nowak, Corina Tarnita, and E. O. Wilson, published in Nature last summer, was getting at the time.  (If you don’t know what I’m talking about, Carl Zimmer has a good write-up about it).  I’d read the paper at the time and dismissed it for largely (as far as I can tell) the same reasons as everyone else did:  it stinks.  And then, I forgot about it.

I was recently reminded, however, by the buzz that is going around right now about the responses to this paper that have just been published by Nature, some seven(!) months later.  Jerry Coyne has blogged about it, and it’s a good read for many reasons not least of which is that he’s an author on one of the critiques along with 136 people, among them some of the biggest names in evolutionary biology and social evolution.  I’d point out some of the people on that list and their accomplishments, but I’d get the same result if I wrote a book on the subject of Nowak et al.’s paper – they’d all be in it.  Honestly, the only question I have about that is how did they organize it?  The critique itself is worth reading as well, if only for the concise beat-down that they apply to the subjects of their wrath.  (D. S. Wilson disagrees, but I think that he’s managed to completely miss the point.  Read and decide for yourself, though.  Full disclosure:  I don’t agree with much of what D. S. Wilson says.)

And the icing on the cake has to be this video, from Jon Wilkins.  I’d love to embed it, but it’s on Xtranormal and WordPress.com apparently doesn’t support embedding from there, so click through and have a good gander.  If you have any interest in this issue, it’s a great video.

Do I have anything to add to this?  Honestly, only a vague sorrow, especially about Nowak.  When I was starting my master’s, I came across the work his lab was doing on evolutionary graph theory and loved it;  it was a great inspiration to me at the time, and it remains so to this day.  But when I read things like this eusociality paper, I see another Nowak, and it’s not a Nowak that I’m particularly enamored of.

An awesome book review … not by me.

1000000487.JPG, a photo by Winawer0 on Flickr.

I got a nice surprise from the UPS man yesterday: my copy of Carlin and Lewis’s Bayesian Methods for Data Analysis. Since I’m going to be joining a lab that’s done a fair bit of Bayesian work and I’m a little light in that area (wait, should I be admitting that?), it seemed like a great excuse to bone up in anticipation of showing up there. But getting me the book reminded me of the great review I say of it on Amazon, which is worth a read for statistical geeks:

Andrew Gelman’s review of the book

The review is by Andrew Gelman, one of the godfathers of Bayesian analysis and a giant in statistical work in general. His blog is also a great resource. The review he wrote about Carlin and Lewis’ book is a classy affair that situates it well against the now-classic text that Gelman helped co-author, and you’ll just have to excuse me while I geek out a little bit.

Wait – I guess you don’t come read a blog about behavioural ecology unless you’re already a geek, so I guess that we’re good there!

Random thought of the day: casual games.

I’ve seen a number of complaints lately from “hardcore” gamers about casual games (e.g. this – definitely NSFW), and it’s led me to wonder if there isn’t a little bit of narrative re-writing going on here.  Casual gaming is definitely an exploding segment of the market – Wikipedia suggests that an estimated 200 million people a month play casual games online –  but therein lies the rub:  perhaps the issue isn’t a sudden shift in the market, but just its massive growth.  Now that gaming is reaching so many more people on so many more platforms, maybe casual gaming just represents an inevitable expansion and not a declining standard.  Or perhaps it’s both.  It’s an empirical question, but I don’t see a lot of data;  if anyone has any thoughts (or evidence!) on the subject, I’d be glad to hear about it.

Overlooked classic paper: Spatial effects in group foraging.

I’ll be defending my thesis in a few months time, and I’ve been re-reading old papers recently to get myself in the right head-space. A few days ago, I came across a paper that I read at the beginning of my Ph.D., but otherwise forgot about until now – which is a shame, because it’s a good paper. Worse, it’s the sort of paper that should have gotten more attention than it did, or at least more attention than I’ve seen it get. This issue, of the endless treadmill of peer-review publications fading into the twilight (sometimes a mere weeks after publication), has been on my mind lately. But that’s the virtue of having this blog: I can dig this paper up and give it some of the attention that it does deserve.

Of course, since I’ve done this a bit clumsily, you have no idea what paper I’m talking about. So, let’s bring it out into the light:

G. D. Ruxton. Foraging in flocks: non-spatial models may neglect important costs. Ecological Modelling, 82:277–285, 1995.

Behavioural ecology is a discipline that has, to date, been largely focused on problems that can be modelled analytically by solving equations or simple games, or perhaps deriving more complicated equations that were solved through numerical methods. But some behavioural situations are not so amenable to these types of analyses, and so we tend to turn to simulation work to help bridge the gap. One such example is group foraging. Foraging models, be they optimal foraging models (where individuals forage individually, even if they do so in a group) or social foraging models (where individuals use information from other foragers to influence their own decisions), have rarely been situated in a spatially-explicit world. The reason for this is simple: spatial models are hard. Simulations are a great way to handle these types of models, and in recent years this has become more common – my own Ph.D. work is a fair example of this! – but in the early-to-mid-90s, this was just in its infancy.

Enter Dr. Graeme Ruxton, who in 1995 wrote the paper above to make the point that ignoring spatial effects in group foraging models was doing a disservice to the understanding of these behaviours. Because I think it’s an important point, and because 15 years later I’m flogging the same point in some of my own work, I’m going to spend a few minutes explaining Ruxton’s model.

A schematic view of the individual-based model.

The model is what would now be called an individual-based model (IBM; also known as Agent-Based Modelling, ABM). Foragers moved across a 1000×1000 regular grid, searching for food patches that were scattered across the grid (see the diagram). When an individual found a food patch, every other searcher abandoned what they were doing and moved toward the food find until every forager was at the same patch. This may sound a little odd – what if the patch was exhausted? – but because the goal was to look at how spatial effects played out in terms of search time and movement time, Ruxton didn’t record feeding rates or any such thing (this issue is explored more thoroughly in a paper published the same year with S. J. Hall and W. S. C. Gurney). If you’re familiar with social foraging models, you may recognize this model as a simple example of an Information-Sharing game; I plan on returning to this theme in a later post.

The point of the paper was to ask what effect various movement strategies would have on the time it took for individuals to find patches. In particular, how long would it take to find the first searcher to find a patch, and how long would it take the rest of the group to converge on that patch? To do this, he explored six different movement rules, of which I’ll present four here. (You can read the paper for the other two; the point here is to discuss the importance of the paper, not replicate it in full).

• A simple random walk. The individual moves in any of the eight possible directions, randomly chosen each turn. All eight directions are equally likely to be chosen as the direction for next turn’s movement.
• A group biased walk: individuals would move more often in a direction chosen at the start of the simulation. For instance, they might prefer to move to the right, so more of their moves will be to the right as opposed to the other seven directions. The strength of the preference is tweakable, and the entire group has the same direction preference.
• An individual biased walk: same as a group biased walk, but every individual has their own preferred direction.
• Site marking: individuals mark sites that they’ve been to, something like ant pheromone trails; searches don’t enter a marked site unless they have nowhere else to go. Site markers fade over time, and the decay time is adjustable.

The paper goes on to explore the effect of these rules on the searching and convergence times, presenting results for each rule and contrasting them with the results from classical models. I’ll mention a couple of the results, but because I’m uncertain as to what I can clip from the paper in terms of figures, I can’t get too deeply into it (now there’s something I need to look into!) and I’d recommend giving the paper a read.

One of the more interesting results relates to the time taken to find a patch as a function of the number of searchers. Classical models expected that this was linear: add more searchers, and your search time goes down in a straight line fashion. But Ruxton’s results showed that adding more searchers might not have such a linear effect, because often new searchers would blindly trample over spaces that previous searchers had already covered. Thus, you might get diminishing returns to search efficiency from adding more searchers. (You can see this in Figure 1b from the paper, which I’ve reproduced here). The rest of the paper explores the individual effects of each of the movement rules, and it’s worth reading for that alone.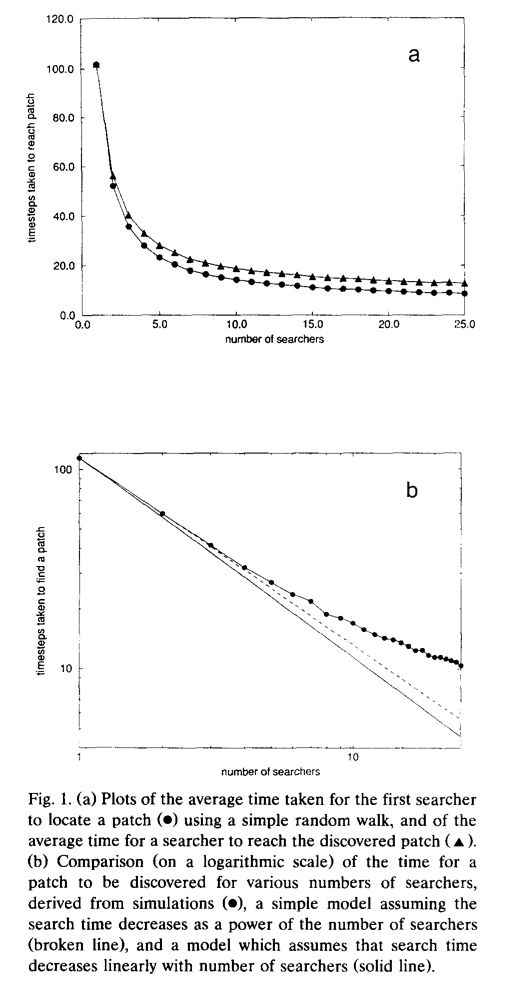

But why is this important? Well, behavioural ecologists studying the evolution of group behaviours like foraging might incorrectly predict – or have trouble explaining – the size of foraging groups based on these search efficiencies. Worse, they might not build these diminishing returns into their models as a cost of increasing group size when trying to explain why individuals form groups and why groups are of a certain size. Because these effects come directly from incorporating spatial structure into the model, classical non-spatial models can’t easily take them into account.

This paper is especially important because it was one of the first – to my knowledge – to make this point so clearly. It’s not the first to argue that spatial effects are important, by any means, but it does so in a way that highlights the importance of these effects to the study of foraging. Unfortunately, despite fits and starts over the years to follow, this lesson is only now starting to take hold in a big way in behavioural ecology (as far as I can see!). I’ll say it: I’d recommend that anyone studying the evolution of foraging behaviour should read this paper, if only because it foresees issues that we’re grappling with right now.

And hey, it’s only 9 pages. Not too bad, right?